はじめに
本記事では、企業価値評価の上で、企業の資本コストを算出するのに必須なレバードベータ・アンレバードベータについて、概念から変換式の算出方法まで網羅的に解説していきます。
加重平均資本コスト(WACC)とは
DCFで企業価値を評価する際には、企業の資本コストを算出する必要があります。一般に、企業の資本コストを算出する際には、負債コストと株主資本コストを資本構成に合わせて加重平均した加重平均資本コスト(WACC)が利用されます。本記事ではWACCの詳細については踏み込みませんが、WACCは一般に下記の式で計算されます。
(参考)WACCの式
\(WACC=\frac{D}{D+E}\times r_{D}\left( 1-T\right) + \frac{E}{D+E}\times r_{E}\)
D:負債額, E:株式時価総額, rD :負債コスト, rE :株主資本コスト, T:実効税率
ベータ(β)とは
WACCの式に含まれる株主資本コストの算出において、「ベータ(β)」という指標は非常に重要な役割を果たします。学術的にも実務的にも、株主資本コストは、資本資産価格モデル(CAPM)のアプローチで産出されることが一般的です。(本記事では、WACCと同様に細部には踏み込まず、式の提示に留めます。)
\(r_{E}=r_{f}+\beta \left( r_{m}-r_{f}\right)\)
rE :株主資本コスト, rf :リスクフリーレート, β :ベータ, rm :株式市場全体の期待収益率
ここで、βは対象の証券と市場ポートフォリオとの関係性を示します。
β = 1の場合は、企業の株価の変動は市場全体と同じ動きになります。β > 1の場合、企業の株価は市場よりも大きく変動します。市場が上昇する時、証券価格もより大きく上昇し、逆に市場が下落する時も大きく下落します。β < 1の場合、証券は市場よりも変動が少ないです。
ベータ(β)の計算式
上場企業のβは下記の式で計算されます。
\(β_{\text{i}} = \frac{\text{Cov}(r_{\text{i}}, r_{\text{m}})}{\text{Var}(r_{\text{m}})}\)
βi:証券iのベータ, Cov:共分散, ri :証券iの収益率,rm :株式市場全体の収益率, Var:分散
各証券の収益率のデータが必要になるため、こちらの式で計算できるベータは上場している企業のものに限られます。
レバードベータ(βL)とアンレバードベータ(βU)
非上場企業のβは、上述の式では計算することができません。そのため、上場している類似企業のβを基に計算されます。しかし、各企業のβは、個別の企業の資本構成の影響を受けているβ(レバードベータβLβL)のため、資本構成が異なる別の企業へそのまま当てはめることはできません。
そこで、類似企業のβLを、その企業が無負債と考慮したβUへ変換し、算出対象企業の資本構成を考慮したβLへ再変換することにより、計算します。
βLとβUの変換式は2種類あり、下記の通りです。
\(1.\beta _{L}=\left[ 1+\left( 1-T\right) \frac{D}{E}\right] \beta _{U}\)
\(2.\beta _{L}=\left[ 1+\frac{D}{E}\right] \beta _{U}\)
レバードベータ(βL)とアンレバードベータ(βU)の関係式の導出式
上記の2.式について、導出式を解説していきます。こちらで解説する導出では、わかりやすさを重視し、導出に必要ないくつかの点を省略し、あくまで概念を理解していただくことを目的としています。
詳細かつ正確な導出式を知りたい方は、後述する文献を参照ください。
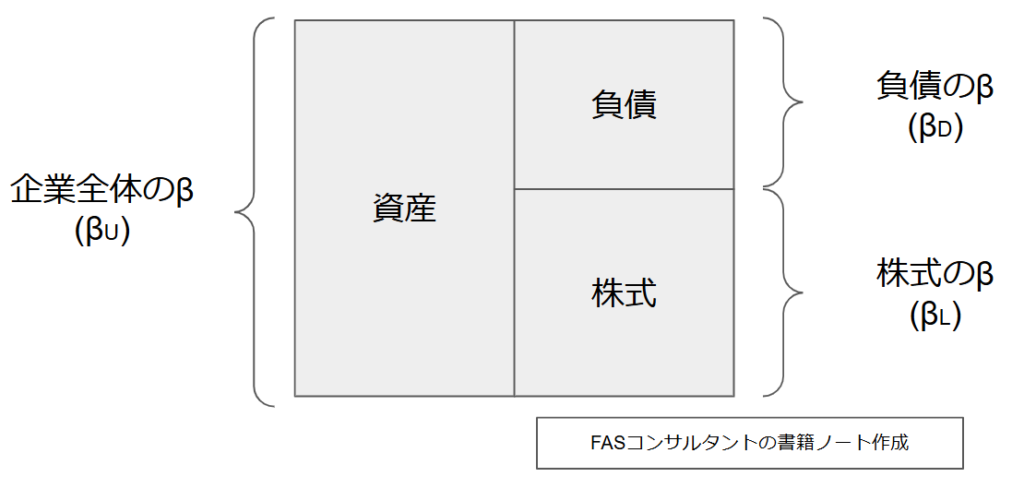
βUは、企業の資本構成を考慮しない、企業全体のβです(図左側)。βUは、負債のベータとβLの加重平均によって決定されます。
\(\beta _{U}=\frac{E}{V}\beta _{L}+\frac{D}{V}\beta _{D}\)
こちらの式を変換すると、下記になります。
\(\beta _{L}=\beta _{U}\times \frac{V}{E}-\beta _{D}\times \frac{D}{E}\)
\(\beta _{L}=\beta _{U}+\left( \beta _{U}-\beta _{D}\right) \times \frac{D}{E}\)
さらに変換し、下記が導出されます。
\(\beta _{L}=\beta _{U}\left( 1+\frac{D}{E}\right) -\beta _{D}\frac{D}{E}\)
負債は株式市場への連動性は低いと考えられるため、負債のβを0と仮定すると下記式が導出されます。こちらの式は上述したβLとβUの変換式の2にあたります。
\(\beta _{L}=\beta _{U}\left( 1+\frac{D}{E}\right)\)
より詳しい導出を知りたい方は、下記が参考になります。
上村昌司「アンレバードベータとレバードベータ」,国際ビジネスファイナンス研究会報告書 第4巻
上記をWebで検索するとPDFの閲覧が可能です。
おわりに
いかがでしたでしょうか。βL、βUの概念と導出式の考え方について解説しました。ご参考になれば幸いです。
当ブログでは、ファイナンスについて解説する記事を掲載しています。
下記は配当についての解説記事です。興味がある方はご覧ください。




